Numbers are Leaves

23 Dec, 2024

Over Christmas I set out to teach myself axiomatic set theory. Specifically, I wanted to teach myself Zermelo-Fraenkel set theory with the axiom of Choice or ZFC.

ZFC consist of a set of axioms initially proposed by Zermelo in 1908 which aimed to build a set theory free of paradoxes like Russell's paradox which led to contradictions making the theory inconsistent[0].

If you don't know why set theory is important, it is because set theory is the foundation of all of mathematics. That is:

• All mathematical concepts can be expressed set-theoretically (e.g. geometry)
• All concrete mathematical objects are specific sets (e.g. a specific line)

Today we'll be looking at constructing whole numbers in set theory and how when they are constructed in an intuitive way, these numbers look shockingly similar to biological leaves we find on trees.

So what are sets?

Informally, a set is simply collections of objects. The elements of a set are also sets. The set with no element is called the empty set $\{\}$, often denoted by $\varnothing$.

Let's define a set $A$ with two elements, $B$ and $C$:

$A=\{B,C\}$

then let's say that $B$ is the empty set:

$B=\varnothing$

and $C$ is the set containing the empty set:

$C=\{\varnothing \}$

then:

$A=\{\varnothing ,\{\varnothing \}\}$

Simple right?

Axiom of Foundation

The Axiom of Foundation states that sets must be well founded. This implies:

1. Sets cannot have infinite depth
2. Sets cannot be members of themselves

Furthemore the Axiom of Foundation implies that sets can be nicely visualised as trees! In set theory $X$ being a member of $Y$ is equivalent to $X$ being a child of $Y$ in the world of trees.

So the tree corresponding to the empty set ∅ is:

the tree corresponding to $C$ above is:

and the tree corresponding to $A$ is:

Representing numbers

Given what we've discussed about set theory so far, if I were to ask you to try to represent the natural numbers (${\displaystyle \mathbb{N}}=\{0,1,2,...\}$) via sets, what encoding would you come up with? Think about it for a second.

The first idea that comes to mind is the following encoding scheme:

$0=\{\}=\varnothing$

$1=\{\varnothing \}$

$2=\{\varnothing ,\varnothing \}$

$3=\{\varnothing ,\varnothing ,\varnothing \}$

etc.

Good idea! Unfortunately this doesn't work due to one of the other axioms of set theory called the Axiom of Extentionality which states that two sets are equal if and only if they contain the same elements. This indirectly enforces the idea that sets cannot have duplicate elements, as set membership is defined purely by the presence or absence of elements. For example:

$\{\varnothing ,\varnothing \}=\{\varnothing ,\varnothing ,\varnothing ,\varnothing \}=\{\varnothing \}$

Hm. What if we recursively define $n+1=\{n\}$ where $0=\varnothing$.

So:

$0=\varnothing$

$1=\{0\}=\{\varnothing \}$

$2=\{1\}=\{\{\varnothing \}\}$

Well congratulations this works! We can represent numbers using singleton sets (sets with one element).

However, it would be nice if our sets had some more structure. Specifically we would like the set corresponding to the number $n$ to have $n$ elements.

Von Neumann Ordinals

One such construction is due to John Von Neumann called the Von Neumann Ordinals. We can define the natural numbers recursively by letting $0=\varnothing$ and the successor of $n$ (so $n+1$) be the union $S(n)=n\cup \{n\}$. With this construction $n=\{0,1,,\dots ,n-1\}$. Concretely:

$0=\{\}=\varnothing$

$1=\{0\}=\{\varnothing \}$

$2=\{0,1\}=\{\varnothing ,\{\varnothing \}\}$

$3=\{0,1,2\}=\{\varnothing ,\{\varnothing \},\{\varnothing ,\{\varnothing \}\}\}$

$4=\{0,1,2,3\}=\{\varnothing ,\{\varnothing \},\{\varnothing ,\{\varnothing \}\},\{\varnothing ,\{\varnothing \},\{\varnothing ,\{\varnothing \}\}\}\}$

Visualising Von Neumann Ordinals

Von Neumann ordinals are defined recursively and are therefore self-similar. Let's look at the trees corresponding to the first few Von Neumann Ordinals.

The number 0 is simply the empty set by definition.

The number 1 is simply the set containing the set containing the empty set.

The number 2 starts to show us a little more structure. 2 is the set containing 0 and 1.

3 Is where the self-similarity really starts to show as 3 contains 0, 1 and 2, which in turn contains 1 and 2.

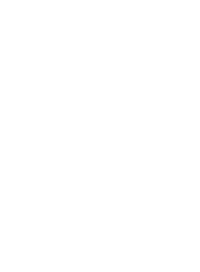
Moving onto 4 the self-similarity becomes even more obvious. Counting up the number of nodes we can start to see a pattern there as well. The number of nodes are exactly $2^n$.

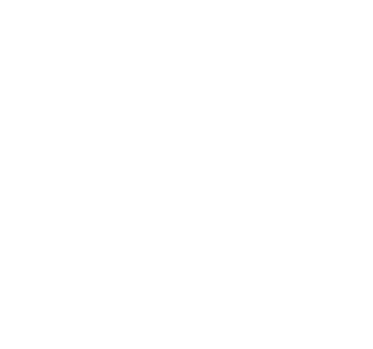
Finally with 5 the self-similarity continues as expected.

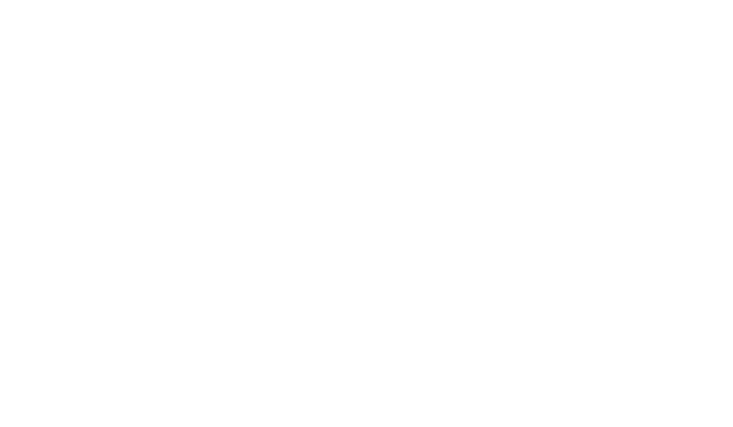
Looking that the trees generated by representing sets as trees and numbers as sets, we can see the recursive self-similarity of the Von Neumann ordinals.

However I did promise you that numbers were leaves, and not trees.

Force-Directed Graph Layouts

The tree visualisations above are rendered using the graph layout engine dot. It's rendering a hierarchical structure where the root of the tree is the parent set, the first level is the root of the children of the parent set, the second is the root of the children's children, etc.

To gain more insight into the symmetrical structure of Von Neumann ordinals, we'll instead be using a Force-Directed graph layout engine.

This is a beautifully simple idea. We simulate Hooke-like forces pulling two nodes which are linked together, and Coulomb-like repulsive forces pushing apart two nodes which are not linked.

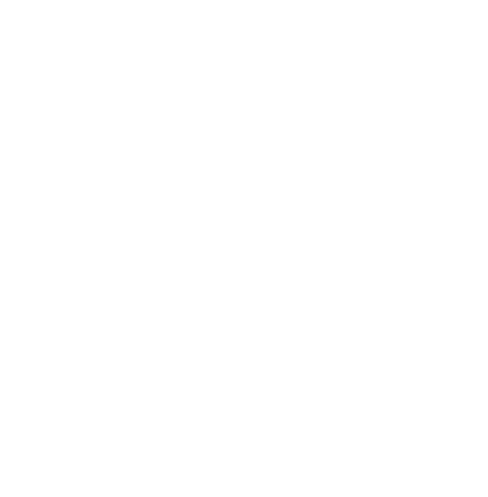
The layout engine sfdp provides this functionality, converting the number 5 from:

to:

Numbers are Leaves

With that introduction, sit back, relax and enjoy as increasingly large numbers become leaves before your very eyes.

6: The Number Six.

7: The Number Seven.

8: The Number Eight.

9: The Number Nine.

10: The Number Ten.

11: The Number Eleven.

12: The Number Twelve.

13: The Number Thirteen.

14: The Number Fourteen.

15: The Number Fifteen.

16: The Number Sixteen.

What's next?

I would like to understand why numbers looks like leaves and not some other fractal like snowflakes for example (the inverse question, why biological leaves have this specific self-similar structure may yield more fruit).

I think a fair thing to ask is if the force-directed layout engine is uniquely responsible for the leaf-like structure and this has nothing to do with the Von Neumann ordinals themselves.

To check this I generated some Collatz trees and they ended up looking like microbes. I think it's safe to say the answer is no.

The next natural step is to look at what rational numbers look like. We can express rational numbers set theoretically as as the set of ordered pairs $\frac{a}{b}=(a,b)$ using Kuratowski's construction $(a,b)=\{\{a\},\{a,b\}\}$ where $a,b$ are Von Neumann ordinals. I suspect they will also look like leaves since they are loose structure over Von Neumann ordinals.

Notes

[0]: Russell's paradox defines the set of all sets that are not a member of themselves. Does this set contain itself?